Klirrfaktor
Als erstes wollen wir ein vorhandenes Wavefile in der Lautstärke anheben. Dies realisiert man durch Multiplikation jedes Abtastwertes mit einem konstanten Faktor, d.h. mit einem Multiplizierer. Zunächst wollen wir das Musicfile aus der 1. Übung um 3, 6 und 9 dB verstärken. Dabei wird es bei hoher Verstärkung zwangsläufig zu einem sogenannten Clipping kommen: Das Produkt aus der Originalamplitude und dem Verstärkungsfaktor ist betragsmäßig größer als der maximal darstellbare Amplitudenwert, d.h. bei 16 bit < -32768 bzw. > 32767. In diesem Fall muß dafür gesorgt werden, daß der resultierende Wert auf genau -32768, bzw. 32767 gesetzt wird. Clipping ist akustisch als immer stärker werdende nichtlineare Verzerrung wahrnehmbar.Bei welcher Verstärkung wird eine Verzerrung beim gewählten Soundfile wahrnehmbar? (Source-Ausschnitt, wave und Ausschnitt mit geclippten Bereichen ins Protokoll).
Ein Maß für die Verzerrung ist der sogenannte Klirrfaktor k, der für eine periodische Schwingung folgendermaßen definiert ist:
k=Effektivwert ohne Grundton/Effektivwert mit Grundton. Der Klirrfaktor läßt sich aus dem Spektrum berechnen. Wir wollen nun eine 1kHz-Sinusschwingung um 6, 9 und 12 dB verstärken und den resultierenden Klirrfaktor berechnen (Spektrogramm des Ausgangsignals mit GRAM berechnen, Plot ins Protokoll).
Sinus 1kHz
Den Effektivwert ohne/mit Grundton einer harmonischen Schwingung berechnet man, indem man die auf die Grundton bezogenen Amplituden der Obertöne quadriert, addiert und aus dem Resultat die Wurzel zieht: Effektivwert_gesamt_mit_Grundton = sqrt( Effektivwert_F0**2 + Effektivwert_2F0**2 + Effektivwert_3F0**2 + ...)
Dazu muß man die dB-Angaben aus GRAM in lineare Angaben zurückrechnen (siehe Aufgabe 2.1).
Modifizierter Code
db_factor3db = 1.4125; // 3dB = 10^(3/20)
db_factor6db = 1.9952; // 6dB = 10^(6/20)
db_factor9db = 2.8184; // 9dB = 10^(9/20)
db_factor12db = 3.9811; // 12dB = 10^(12/20)
new_wave = (short*)malloc(n_wave*sizeof(short));
for(i=0; i < n_wave; i++) {
float temp = wave[i] * db_factor3db;
if (temp > 32767) {
wave[i] = 32767;
} else if (temp < -32768) {
wave[i] = -32768;
} else {
wave[i] = (short)temp;
}
}
Musik: Verstärkung um 6 dB
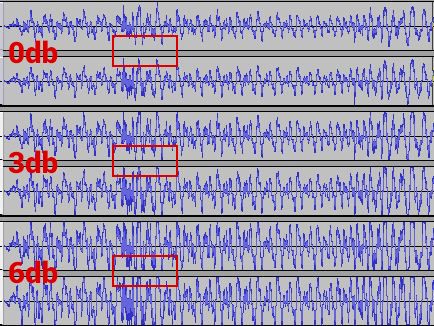
Abbildung: Bei einer Verstärkung um 6 dB ist die Verzerrung wahrnehmbar. Ab 3dB tritt Clipping auf.
Sinus 1kHz Verstärkungen
0dB Verstärkung

Abbildung: Verstärkung von Sinus 1kHz mit 0dB
6dB Verstärkung
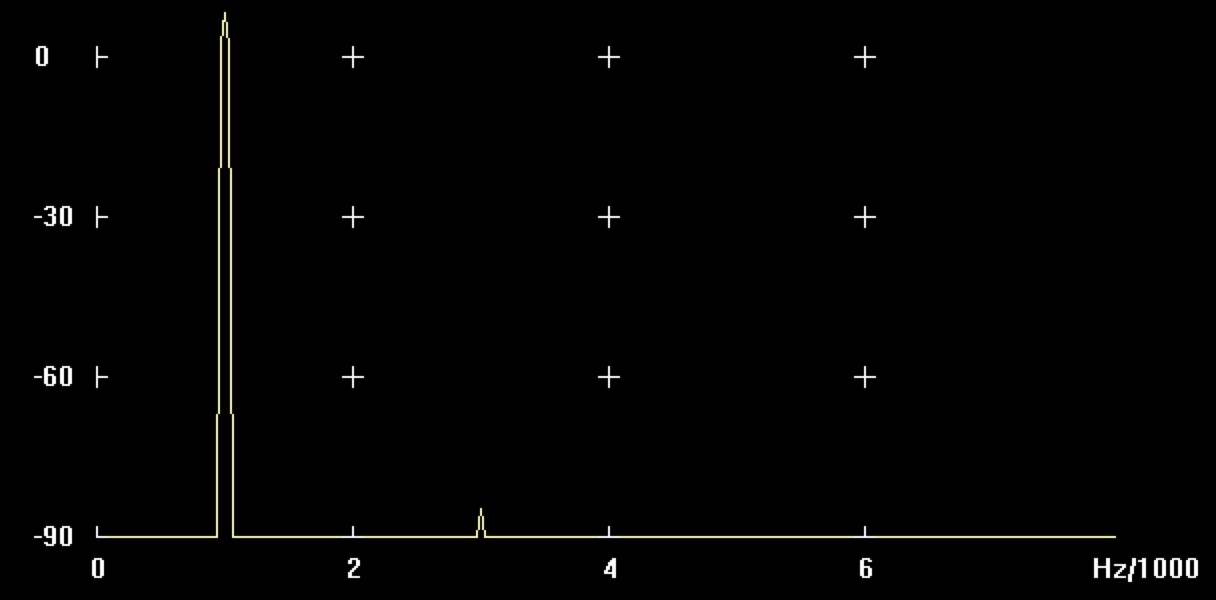
Abbildung: Verstärkung von Sinus 1kHz mit 6dB
9dB Verstärkung
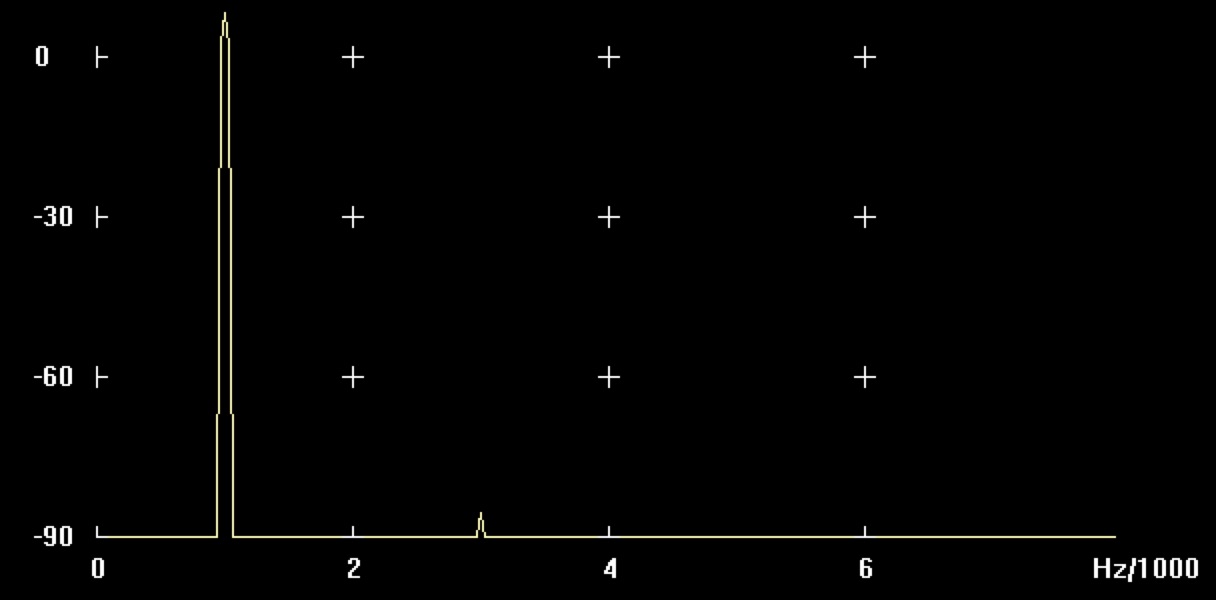
Abbildung: Verstärkung von Sinus 1kHz mit 9dB
12dB Verstärkung
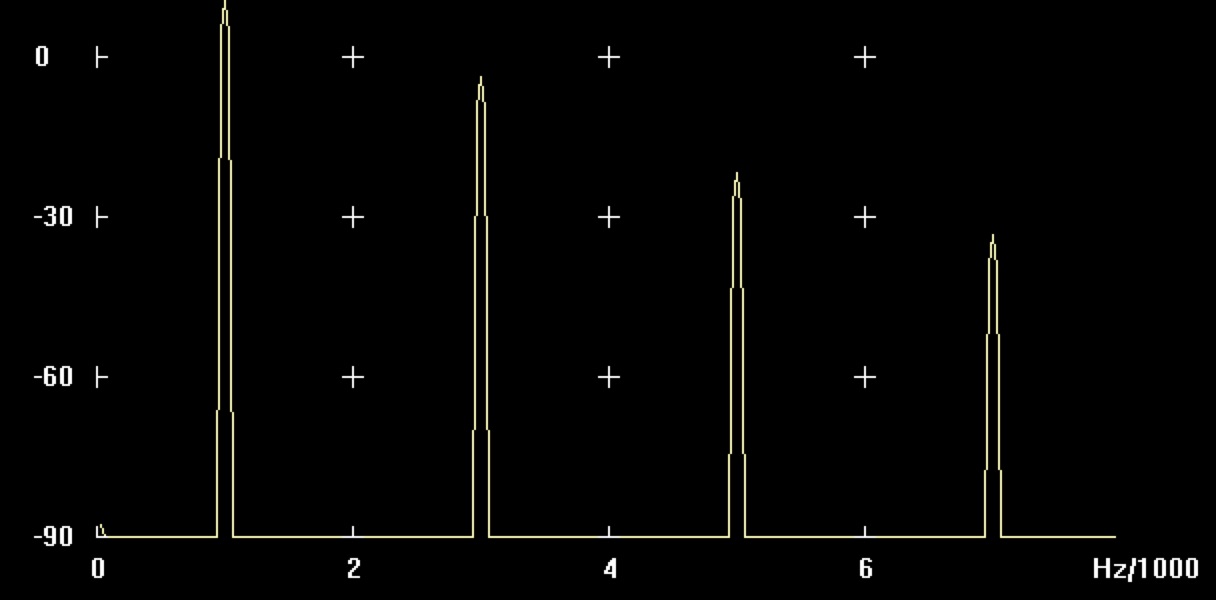
Abbildung: Verstärkung von Sinus 1kHz mit 12dB
| Frequenz (Hz) | Lautstärke (dB) | Oberwelle (dB) | Prozent (%) |
|---|---|---|---|
| 1000 | -3,5 | ||
| 3000 | -18 | -14,5 | ca. 19 |
| 5000 | -36 | -32.5 | ca. 2 |
| 7000 | -47 | -43,5 | ca. 1 |
Berechnung des Klirrfaktors (allgemein):
Klirrfaktor k = (Effektivwert_ohne_Grundton) / (Effektivwert_mit_Grundton)
Effektivwert = sqrt(Effektivwert_1F02 + Effektivwert_2F02 + Effektivwert_3F02 + ...)
Berechnung unseres Klirrfaktors:
Klirrfaktor k = sqrt ((0,18822 + 0,02322 + 0,00072)/ (12 + 0,18822 + 0,02322 + 0,00072)) = 0,1863
Echo
Ein wichtiger Effekt in der Studiotechnik ist das Echo. Dabei wird zu einem Signal eine zeitverzögerte und in der Amplitude gedämpfte Überlagerung hinzugemischt: y(k)=x(k)+a*x(k-T), wobei T eine ganze Zahl zwischen 1 und N sein kann. Wir wollen WAVE_IO so modifieren, daß wir eine Verzögerung von 10 bzw 200 ms erreichen. Um wieviele Abtastwerte müssen wir verzögern, wenn wir mit einer Abtastrate von 44.1 kHz arbeiten ? Wir setzen a auf 0.6. Wende das Echo auf ein Sprach- und ein Musiksignal an. Es kann sein, dass die 10ms nur bei einem recht trockenen Soundfile wie der Sprachaufnahme hörbar werden (Waves original und mit Echo, Programm-Source ins Protokoll). Hinweis: Bei Stereodateien müssen wir berücksichtigen, daß linker und rechter Kanal getrennt verzögert werden müssen. Die Samples für links und rechts liegen im Array wave jeweils hintereinander.Modifizierter Code
n = 0.01 * freq_in; // 10ms
//n = 0.2 * freq_in; // 200ms
a = 0.6;
new_wave = malloc(n_wave * sizeof(short));
for (i = 0; i < n_wave; i++) {
if (i >= n) {
new_wave[i] = 0.5 * wave[i] + (short)((float)(wave[i - n]) *a);
}
else {
new_wave[i] = wave[i];
}
}
Das n steht für die Anzahl der Verzögerungsglieder und das a für den Faktor des Echos. Wir addieren auf das Original das Echo (16 Bit + 16 Bit = 32 Bit). Um eine Übersteuerung zu vermeiden multiplizieren wir mit 0.5.
Musik: 0ms
Musik: 10ms
Musik: 200ms
Sprache: 0ms
Sprache: 10ms
Sprache: 200ms
Einfacher Filter
Ein sehr einfaches Filter kann man z.B. mit der Zuordnungsvorschrift (a) y(k)=0.5*x(k)+0.45*x(k-1) realisieren. Programmiere das Filter und vergleiche eine Musicdatei vor und nach der Filterung. Tue dasselbe mit der Zuordnungsvorschrift (b)y(k) = 0.5 * x(k) - 0.45 * x(k-1). Um was für eine Art Filter handelt es sich jeweils ? (waves Original, Filter a) und b) ins Protokoll)
Zum Testen unserer Filter verwenden wir Weißes Rauschen
das alle Frequenzen enthält. Wenn wir nun das Original-Spektrum (oben) mit den gefilterten vergleichen, sollte sich ein Bild wie in der Mitte und unten ergeben, anderenfalls ist etwas mit dem Programm nicht in Ordnung (welcher Output von welchem Filter stammt, wird nicht verraten ! Das müßt Ihr selber herausfinden.) Um eine Glättung des Spektrums zu erzielen, bei GRAM 'Spectrum Average' auf 100 setzen. (Plots der eigenen Spektren ins Protokoll !)
for (i = 0; i < n_wave; i++) {
//Tiefpass
float temp = 0.5*wave[i] + 0.45*wave[i - 1];
//Hochpass
//float temp =0.5*wave[i] - 0.45*wave[i-1];
wave[i] = (short)temp;
}
Weisses Rauschen
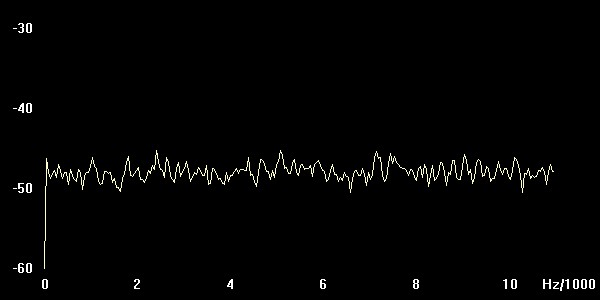
Abbildung: Weisses Rauschen
Tiefpass
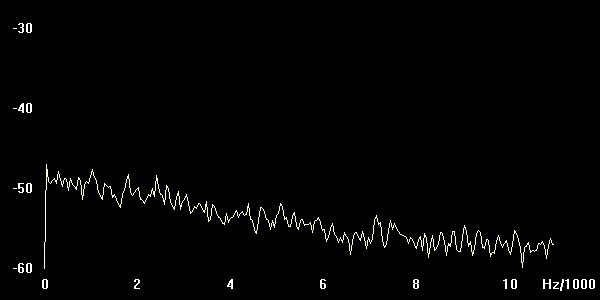
Abbildung: Tiefpass
Hochpass
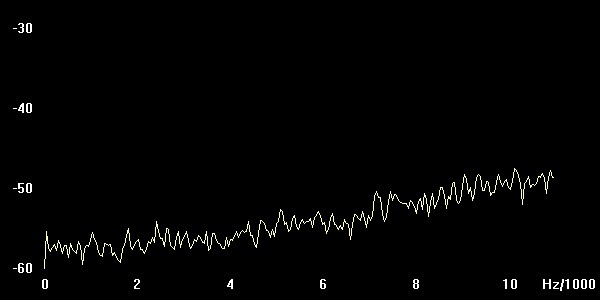
Abbildung: Hochpass