Einfache Schwingungsformen
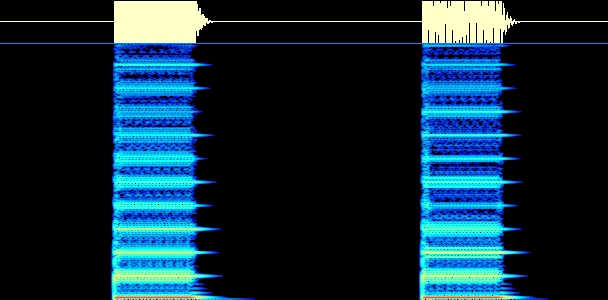
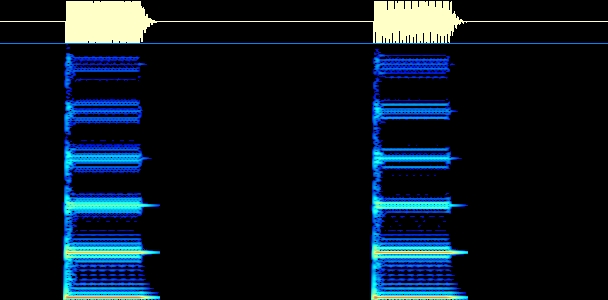
Zunächst brauchen wir nur ein PitchGate und einen Oszillator. Im Ensemble-View fügen wir ein Oszilloskop ein, mit dem wir das Zeitsignal des Klangs darstellen können. Nun schauen wir uns die Wellenformen der Grundklänge des Oszillators an (Sägezahn, Rechteck, etc.). Wir können nun Beispiele der einzelnen Klänge in Reaktor aufzeichnen. Über das Menü "View->Show Recorderbox" exportieren wir die Klänge als wav und lesen sie in GRAM über 'Scan File' ein. Um das Spektrum anzuzeigen, müssen wir den Display-Type "Line" auswählen. Es erscheint eine Liniendarstellung des Amplitudenspektrums mit dB-Angaben (Toggle Grid). Aus diesen können wir dann lineare Prozentwerte mit Bezug auf die Grundschwingung berechnen. Wir setzen dazu die Grundschwingung mit 0 dB entspr. 100 % an. Variiere die Pulsweite (d.h. das zeitl. Verhältnis zwischen positivem und negativem Schwingungsteil) bei der Rechteckschwingung (Regler `P-Width´ am Oszillator) und beobachte, wie sich das Verhältnis der Obertöne verändert. (Ins Protokoll: Plots der Spektren für drei markante P-Width-Einstellungen beim Rechteck, ein Sägezahn, ein Dreieck, Ausschnitte aus den wavs, Angaben der Frequenzen und Amplituden in dB und Prozentwerten für die Grundschwingung und die ersten drei Obertöne, bei denen die Amplitude größer 0 ist). Wir können in GRAM auch "online" das Spektrum des Synthesizerklangs darstellen, d.h. während wir spielen. Dazu wählen wir 'Scan Input', stellen eine Samplingfrequenz von 5.5. kHz und 'Mono' ein. Damit das Signal erscheint, muss im Windows-Mixer "Was Sie hören" als Quelle ausgewählt sein.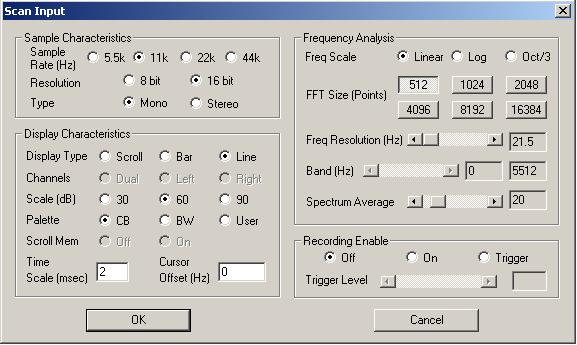
Abbildung: Gram Einstellungen
Die Formel für die Berechnung des Verhältnisses zur Amplitude (An) in %
lautet:
20 * log(An / A1)
Triangle P-Width 50
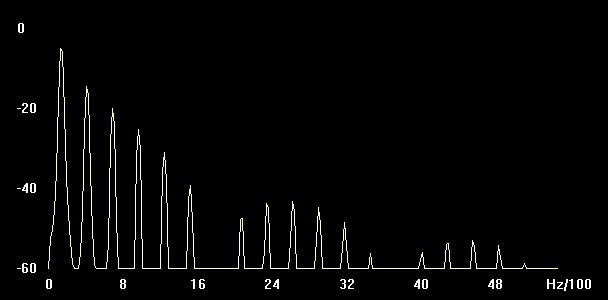
Abbildung: Triangle P-Width 50 Messung
| Teilton | Frequenz (Hz) | An (dB) | Unterschied zu A1 (dB) | Verhältnis zur Amplitude (%) | |
|---|---|---|---|---|---|
| in Hz | in dB | in dB | als Verhältnis | in % | |
| 1 | 140 Hz | -5 | 0 | 0 | 0 |
| 2 | 409 Hz | -15 | -10 | 0,3162 | 32% |
| 3 | 689 Hz | -20 | -5 | 0,5623 | 56% |
| 4 | 969 Hz | -25 | -5 | 0,5623 | 56% |
Sägezahn P-Width 50
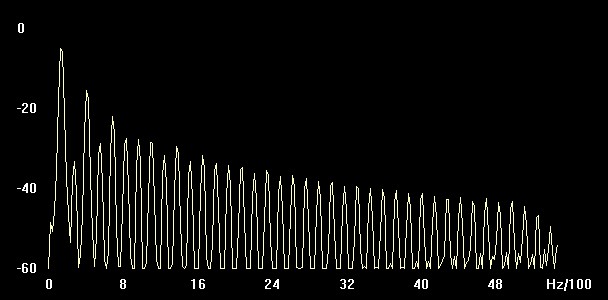
Abbildung: Sägezahn P-Width 50 Messung
| Teilton | Frequenz (Hz) | An (dB) | Unterschied zu A1 (dB) | Verhältnis zur Amplitude (%) | |
|---|---|---|---|---|---|
| in Hz | in dB | in dB | als Verhältnis | in % | |
| 1 | 129 Hz | -5 | 0 | 0 | 0 |
| 2 | 280 Hz | -34 | -29 | 0,0354 | 4% |
| 3 | 398 Hz | -15 | -10 | 0,3162 | 32% |
| 4 | 549 Hz | -29 | -24 | 0,0630 | 6% |
Pulse P-Width 0
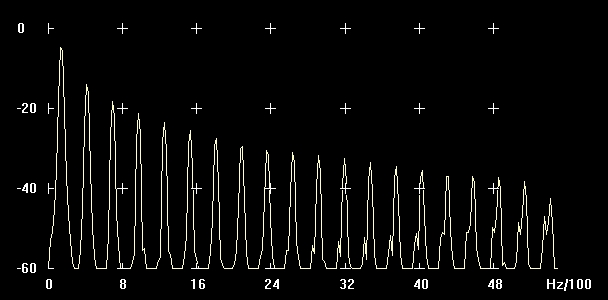
Abbildung: Pulse P-Width 0 Messung
| Teilton | Frequenz (Hz) | An (dB) | Unterschied zu A1 (dB) | Verhältnis zur Amplitude (%) | |
|---|---|---|---|---|---|
| in Hz | in dB | in dB | als Verhältnis | in % | |
| 1 | 129 Hz | -5 | 0 | 0 | 0 |
| 2 | 409 Hz | -14 | -9 | 0,3548 | 36% |
| 3 | 700 Hz | -18 | -13 | 0,2238 | 22% |
| 4 | 969 Hz | -21 | -16 | 0,1584 | 16% |
Pulse P-Width 50
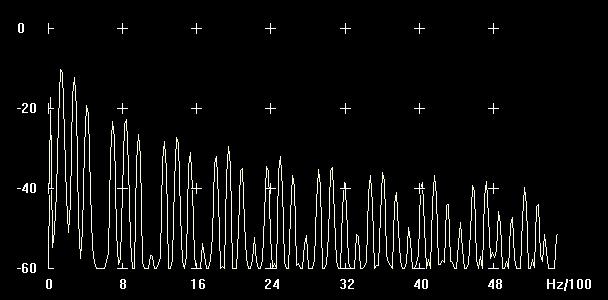
Abbildung: Pulse P-Width 50 Messung
| Teilton | Frequenz (Hz) | An (dB) | Unterschied zu A1 (dB) | Verhältnis zur Amplitude (%) | |
|---|---|---|---|---|---|
| in Hz | in dB | in dB | als Verhältnis | in % | |
| 1 | 129 Hz | -10 | 0 | 0 | 0 |
| 2 | 280 Hz | -12 | -2 | 0,7943 | 80% |
| 3 | 420 Hz | -19 | -9 | 0,3548 | 36% |
| 4 | 689 Hz | -24 | -14 | 0,1995 | 20% |
Pulse P-Width 98
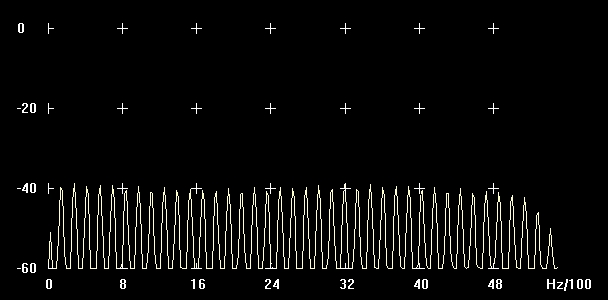
Abbildung: Pulse P-Width 98 Messung
| Teilton | Frequenz (Hz) | An (dB) | Unterschied zu A1 (dB) | Verhältnis zur Amplitude (%) | |
|---|---|---|---|---|---|
| in Hz | in dB | in dB | als Verhältnis | in % | |
| 1 | 140 Hz | -40 | 0 | 0 | 0 |
| 2 | 280 Hz | -39 | 1 | 1,112 | 111% |
| 3 | 420 Hz | -39 | 1 | 1,112 | 111% |
| 4 | 560 Hz | -39 | 1 | 1,112 | 111% |
Schwebung
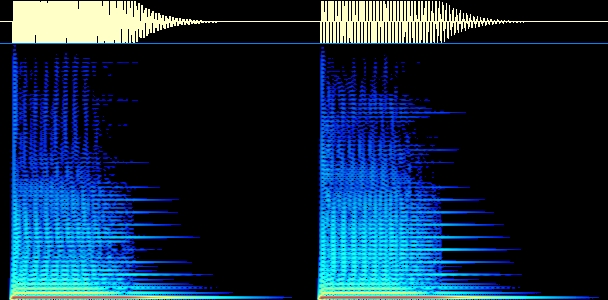
Nun bringen wir einen zweiten Oszillator zum Einsatz. Um die Ausgänge der beiden Oszillatoren anschließen und in der Lautstärke regeln zu können, benötigen wir eine Mixing Matrix 2x2, von der wir allerdings den zweiten Ausgang löschen können. Zunächst stellen wir beide Oszillatoren auf exakt dieselbe Frequenz und Dreiecksschwingung. Dann verstimmen wir den zweiten gegen den ersten und zeichnen den Klang auf, wenn wir gerade eine Amplitudenmodulation feststellen (Fall A), d.h. einen in der Lautstärke schwankenden Ton. Wir verstimmen die Oszillatoren weiter gegeneinander, bis wir den Eindruck einer Dissonanz haben (Fall B), d.h. es entsteht ein rauher, unangenehmer Klang. Beachte, dass der Regler 'Pitch' den betreffenden Oszillator in etwa um Halbtöne verstimmt, während 'Fine' dies um Bruchteile von Halbtöne tut. Am besten experimentiert man zunächst mit dem 'Fine'-Regler und erst, wenn z.B. bei Fall B sich der gewünschte Effekt nicht einstellt, mit dem 'Pitch'-Regler. Nun stellen wir mit GRAM für die beiden Fälle die Frequenzen der Schwingungen fest. Es kann sein, dass die Genauigkeit von GRAM beim Fall A zur Bestimmung der Differenzfrequenz nicht ausreicht. Man kann die Differenzfrequenz aber auch aus dem Oszillogramm der amplitudenmodulierten Schwingung berechnen (z.B. in Samplitude anschauen). Die Periodendauer entspricht nämlich exakt dem Abstand zwischen zwei Punkten maximaler (oder minimaler) Amplitude. Ins Protokoll für beide Fälle: Mittenfrequenz und Differenzfrequenz, Spektrogramm und wav.Amplitudenmodulation
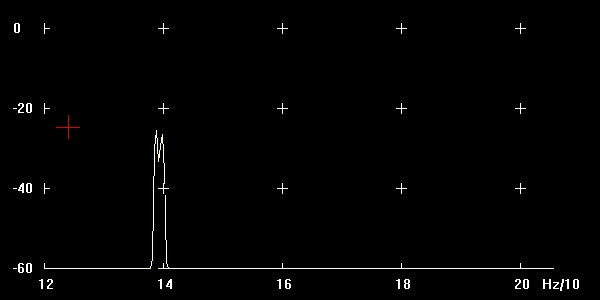
Abbildung: Schwebung Messung
Messungen A:
Amplitude 1: 134 Hz
Amplitude 2: 135 Hz
Mittenfrequenz: (134 + 135) / 2 = 134,5
Differenzfrequenz: 135 - 134 = 1
Dissonanz
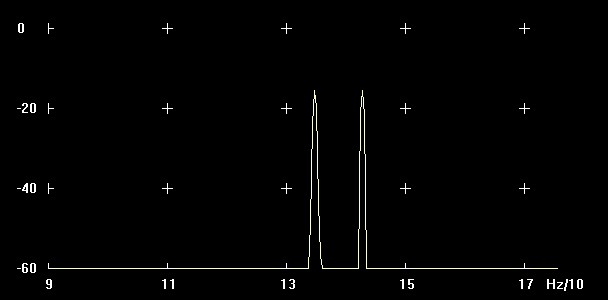
Abbildung: Schwebung Messung
Messungen B:
Amplitude 1: 134 Hz
Amplitude 2: 142 Hz
Mittenfrequenz: (134 + 142) / 2 = 138
Differenzfrequenz: 142 - 134 = 8
Klangnachbildung
Wir wollen nun versuchen, einen der folgenden Klänge nachzuahmen Flöte, Klavinett, Geige. Zunächst wählen wir die Grundwellenform (Rechteck, Sägezahn, etc.), die klanglich am besten zu unserem Instrument paßt (auch mit dem Filter experimentieren ! ). Um die Hüllkurve entsprechend manipulieren zu können, brauchen wir ein ADSR-Makro, das wir zwischen dem Pitch-Gate und den Oszillatoren, allerdings nur in der Gate-Weg einbauen. Damit versuchen wir zunächst den zeitlichen Verlauf des Naturklangs nachzubilden. Vibrato-Effekte lassen sich, wie wir bereits in der Vorlesung gesehen haben, mit LFOs erzielen. Auch Rauschgeneratoren (Anblasgeräusche !) lassen sich in unseren Synthesizer integrieren. Ins Protokoll: Endgültige Struktur des Synthesizers Ensemble-Datei, Klangprobe als wav, Hüllkurve als Plot.Da wir so im Schwung waren und die Aufgabe sehr viel Spaß gemacht hat, haben wir alle 3 Klänge versucht zu erwischen.
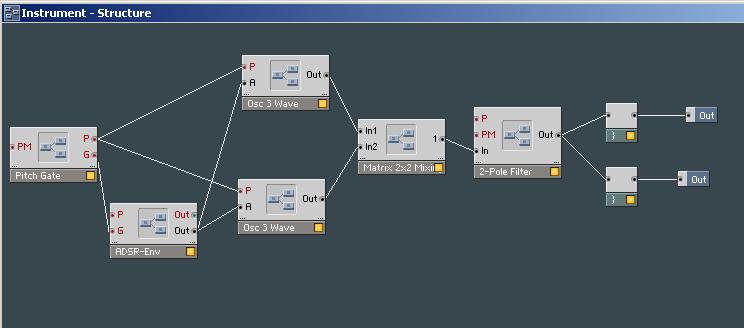
Abbildung: Struktur unseres Synthesizers